Quantum Cognition

Flexible nature of natural concepts and their combinations

The main argument for applying the formal apparatus of quantum theory to the domain of cognition has to do with the flexibility, instability, and context-dependency of natural concepts that manifest themselves as fleeting contents of conscious experience. For example, in the domain of language, words are floating freely in a polyvalent state representing a variety of different uses. As the properties of small particles are not absolute and determined until observing them, the properties of word tokens are not determined until conscious apprehension. Similarly, impressions, ideas and opinions are conceptual entities with analogous properties and likewise invite an analysis in terms of quantum theory.

As suggested by the pioneers of quantum cognition (e.g. Gabora & Aerts 2002, Khrennikov 1999) the quantum formalism can be used to describe the flexible nature of concepts and their combinations in a very simple way in terms of interference effect. This solves well-known puzzles of adjectival modification - such as what is the colour of a red apple (contrasting with the colour of a red flag or red bean (Blutner 2007).  Further, it suggests a new approach to several puzzles of bounded rationality (Franco 2007).

Decision making

There are paradoxical violations of the sure thing principle (Savage 1954)which have resisted explanation by classical decision theory for over a decade. Pothos & Busemeyer (2009) demonstrate that a quantum probability model using Schrödinger's equation provides an elegant of the puzzle. It is convincingly argued that quantum probability provides an appropriate framework for modelling human decision processes.

Quantum musicology

The concept of symmetry plays an important role in many areas of science, including classical mechanics, quantum mechanics, chemistry, crystallography, and theoretical biology. In music, it is indispensable for a mathematical understanding of modulation theory and counterpoint (Mazzola 2002: The topos of music. Birkhauser, Basel). Mathematically, a symmetry is simply a set of transformations applied to given structural states such that the transformations preserve the properties of the states. In music, the most basic symmetry principle is the principle of translation invariance. It says that the musical quality of a musical episode is essentially unchanged if it is transposed into a different key. Such transpositions are mathematically represented by the operations of the cyclic group.

Tonal attraction is a puzzling phenomenon. How well does a given pitch fit into a tonal scale or tonal key, let it be a major or minor key? A similar question can be asked regarding chords and tonal regions. Structural and probabilistic approaches in computational music theory have tried to give systematic answers to this problem of tonal attraction. Recently, a quantum model of tonal attraction has been proposed. It is argued that the quantum approach integrates the insights from both group theory and quantum probability theory. In this way, it achieves a deeper understanding of the cognitive nature of tonal music, especially concerning the nature of musical expectations (Leonhard Meyer) and a better understanding of the affective meaning of music.

  • Blutner (2015): Modelling tonal attraction: Tonal hierarchies, interval cycles, and quantum probabilities.

    Tones are modelled in a qubit space. A Strict correspondence between the circle of fifth and the Bloch sphere is established.
  • Blutner (2016): Musical forces and quantum probabilities.

    Musical forces are derived from local phase shifts in an underlying grid of wave functions.

  • beim Graben & Blutner (2018): Quantum approaches to music cognition

    A Field theory of tonal music is developed. Musical forces are due to deformations of an underlying configuration space.
  • Blutner (2018): Towards a bare-bone semantics for pure music

    A connection between tonal music and its affective response is developed based on ideas of Meyer (1956) and Russell (1979)
  • Blutner and beim Graben (in preparation): Musical Forces and Two Quantum Models of Tonal Attraction

    Deformation of configuartion space and local phase shifts are two possibilities to introduce musical forces in quantum musicology. Both approches are discussed in direct comparison relative to musical data. 

    Quantum field theory of intelligence

    Based on earlier works starting in the 80ies of the last century, Weiss & Weiss (2003) propose a quantum field theory of intelligence. In this approach, the mind-brain has to be seen as a unitary cavity resonator by explicitly exploiting Bose-Einstein statistics (building on ideas of Pascual-Leone). One remarkable hypothesis is that the principle of information coding by the mind-brain is based on the golden mean.

    Mental timing

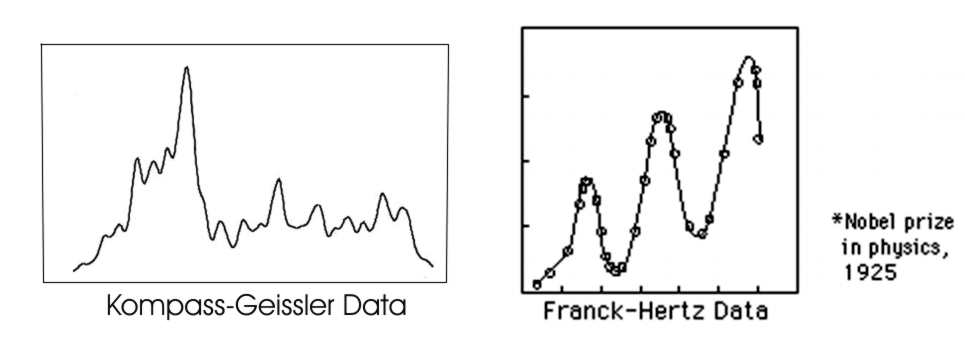
    Starting in the eighties of the last century Geissler and his collegues  formulated a taxonomic model of quantal timing which is based on the entrainment of temporal intervals. The inspection of many different experimental findings suggested that all distinct times are multiples of a small value of about 4.6 ms. A study of apparent motion of Gamma type (Kompass & Geissler 2004)  resulted in experimental distributions  that show close analogies to the famous Franck/Hertz experiment in physics − demonstrating that electrons occuppy only discrete, quantized energy states.

    comparison

    First vs third person accounts

    From the first-person-perspective, phenomenal states of consciousness are multiple realized by neural activation states of the brain, thereby inducing particular partitions of the neural state space. Likewise, physiological measurements of neural activity through EEG/ERP, MEG, PET or fMRI from the third-person-perspective provide a coarse-graining of neural activation patterns that also leads to partitions of the neural state space. In general, these induced partitions will be incompatible to each other, supporting Velmans (2002).

    Fock space representations of cognitive processes

    Many particle systems in quantum physics are described by Fock space states, which are direct sums of tensor product states of arbitrary rank. Such states can represent cognitive data structures such as lists, trees, or frames. A natural way to realize cognitive Fock space representations by neural networks is provided by function spaces in dynamic field theory (Thelen et al. 2001). Appropriately chosen function systems such as spherical harmonics exhibit recursion properties (through Clebsch-Gordan coefficients) that allow for infinite combinatorial productivity as required for neural realizations of cognitive architectures.

    Bistable perception

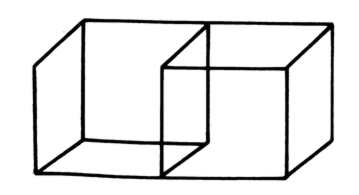
    Quantum Cognition suggests a new and principled way to formalize the distinction between semantic ambiguity and semantic nonspecificity in terms of mixture and superposition, respectively, as first proposed by Jay Atlas (2005). Psychologists have described multistable figures such as the ambiguous maiden/hag drawing and the famous Necker cube. As Atlas points out, there is an important difference between these two examples: the former counts as real ambiguity, but the latter as nonspecificity. An ambiguous figure (or sentence) does not spontaneously perform semantic flips but a nonspecific one does. Moreover, only in cases of nonspecificity one finds the free combination of readings such as the 4 readings of Atlas’ double Necker cube.

    double Necker cube

    Empirical verification of Atlas' view has been provided by Philipp Koralus' (2010) PhD: Semantics in Philosophy and Cognitive Neuroscience: the Open Instruction Theory of Attitude Report Sentences, Descriptions, and the Necker Cube.

    The Necker cube is a paradigmatic example for bistable perception where pattern reversal obeys a particular probability distribution. Atmanspacher, Filk and Römer (2004) discussed this switching dynamics in terms of the quantum Zeno effect where “observation” (here attending to a percept) increases the dwell-time of an otherwise fast decaying unobserved state.

    More relevant publications you can find on Elio Conte's website http://www.saistmp.com/

    Opinion forming and personality psychology

    Aerts et al. (2008) have applied a quantum analysis to a cognitive setting where individuals’ opinions were probed. Three different questions for the opinion poll were considered:

    Q1 : Are you in favour of the use of nuclear energy?
    Q2 : Do you think it would be a good idea to legalize soft-drugs?
    Q3 : Do you think capitalism is better than social-democracy?

    Interestingly, in such situations, most people don’t have a predetermined opinion. Instead, the opinion is formed to a large extent during the process of questioning in a context-dependent way. Personality tests can be seen as a related cognitive setting where individual opinions are probed (Blutner & Hochnadel 2009). 

    Further applications

    They concern the geometry of information retrieval (Widdows 2003; Van Rijsbergen 2004), the semantics of questions (Blutner 2011), Hilbert space semantics and nonmonotonic logic (Engesser & Gabbay 2002)
We recommend RBWD Hedgehog CMS.